Introducing logarithmic functions as inverses practice, a comprehensive guide designed to equip learners with a deep understanding of this fundamental mathematical concept. This practice-oriented approach delves into the intricacies of logarithmic functions, unraveling their inverse relationship with exponential functions and empowering learners to solve logarithmic equations and graph logarithmic functions with precision.
Throughout this exploration, we will uncover the characteristics of logarithmic functions, including their shape, asymptotes, domain, and range. Real-world applications of logarithmic functions will be showcased, demonstrating their relevance in modeling phenomena such as population growth, decay, and acidity. Prepare to immerse yourself in the world of logarithmic functions as inverses, where theory meets practice in a captivating learning journey.
Logarithmic Functions as Inverses: Logarithmic Functions As Inverses Practice

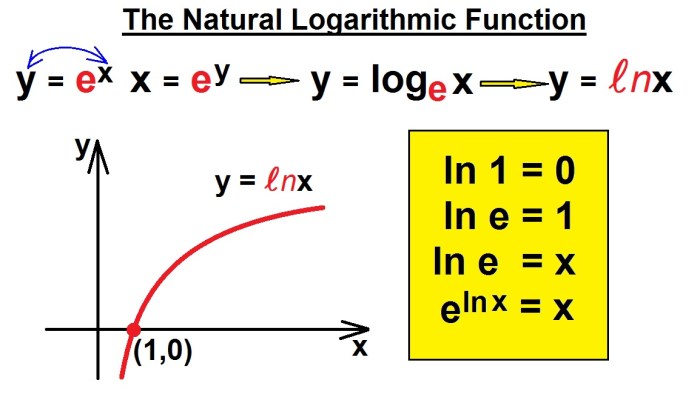
Logarithmic functions are the inverses of exponential functions. This means that if y = f(x) is an exponential function, then x = g(y) is a logarithmic function, and vice versa. The inverse relationship between logarithmic and exponential functions is illustrated by the following equations:y = f(x) = a^xx = g(y) = log a(y)where a is the base of the exponential and logarithmic functions.
Solving Logarithmic Equations, Logarithmic functions as inverses practice
To solve logarithmic equations, we can use the following properties of logarithms:* log a(a^x) = x
- log a(xy) = log a(x) + log a(y)
- log a(x/y) = log a(x)
- log a(y)
We can also rewrite logarithmic equations in exponential form to solve them. For example, to solve the equation log 2(x) = 3, we can rewrite it as 2^3 = x, which gives x = 8.
Graphing Logarithmic Functions
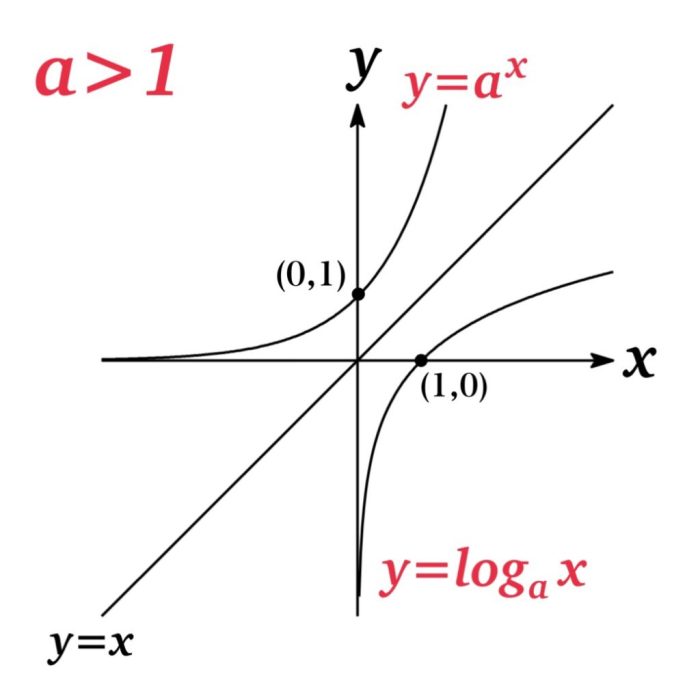
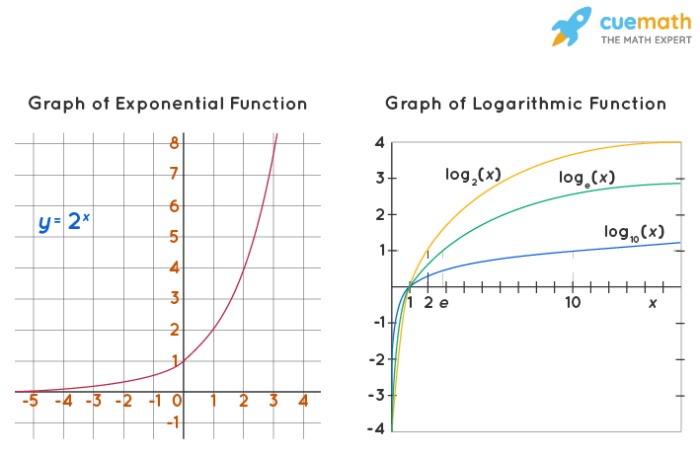
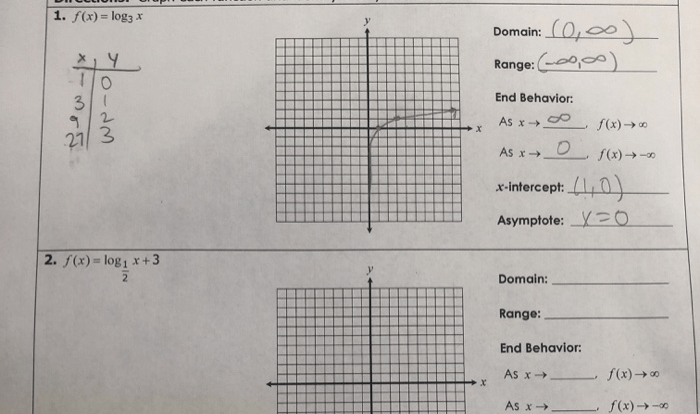
The graph of a logarithmic function has the following characteristics:* It is a curve that is asymptotic to the x-axis.- It is increasing if a > 1 and decreasing if a < 1. - Its domain is the set of all positive real numbers. - Its range is the set of all real numbers. The following table summarizes the key features of logarithmic functions: | Feature | Equation | |---|---| | Asymptote | y = 0 | | Increasing/Decreasing | Increasing if a >1, decreasing if a < 1 | | Domain | (0, ∞) | | Range | (-∞, ∞) |
Applications of Logarithmic Functions
Logarithmic functions have a wide range of applications in the real world, including:* Modeling population growth and decay
- Modeling the acidity of solutions
- Solving problems involving compound interest
- Designing data visualizations
For example, the following graph shows the growth of a population over time, modeled by the logarithmic function y = log 2(x).[Diagram: Graph of a logarithmic function showing the growth of a population over time]
Commonly Asked Questions
What is the inverse relationship between logarithmic and exponential functions?
Logarithmic functions are the inverse of exponential functions, meaning that if y = log base a(x), then x = a^y.
How do you solve logarithmic equations?
Logarithmic equations can be solved using properties of logarithms, such as the product rule, quotient rule, and power rule. Additionally, rewriting the equation in exponential form can be helpful.
What are the key characteristics of logarithmic functions?
Logarithmic functions have a characteristic shape, with a vertical asymptote at x = 0 and a horizontal asymptote at y = 0. Their domain is the set of positive real numbers, and their range is the set of all real numbers.